publications

2026

1. SCA/HPCA ’26

   High-Performance in-Situ ML Inference with Dalotia: A Lightweight Tensor Loader API for Science Codes

   Theresa Pollinger and Jens Domke

   In Proceedings of the Supercomputing Asia and International Conference on High Performance Computing in Asia Pacific Region, New York, NY, USA, 2026

   Abs DOI Bib Code Data

   With the increasing capabilities of machine-learning (ML) systems, the domains of simulation and ML are growing closer together. In particular, the evolving field of ML-based surrogate modeling within turbulence simulations often relies on explicit interfacing between scientific codes and ML frameworks. In the face of increasing hardware and software complexity, it is important to critically assess this approach and to explore alternatives that allow for a tighter integration of simulation and ML. We develop a tensor loading library, dalotia, that allows researchers to embed ML inference directly into their HPC code (“in-situ”) using C, C++, or Fortran. Using dalotia, we evaluate the in-situ approach against inference with ML frameworks (PyTorch, libTorch, and oneDNN). Our experiments using state-of-the-art ML surrogate architectures present complex tradeoffs between convenience, performance, memory usage, energy, and dependency complexity. The data shows that small-batch neural networks can save a factor of 5x in memory overheads when using the in-situ approach. We further observe in-situ speedups of up to 8x compared to the libTorch implementation on the node scale (48 cores). Thus it can be beneficial, in many regards, to rely on native in-situ implementations, without the need for bloated ML frameworks and their dependencies.

   @inproceedings{pollingerHighperformanceInsituML2026a,
     title = {High-Performance in-Situ {{ML Inference}} with Dalotia: {{A Lightweight Tensor Loader API}} for {{Science Codes}}},
     shorttitle = {High-Performance in-Situ {{ML Inference}} with Dalotia},
     booktitle = {Proceedings of the {{Supercomputing Asia}} and {{International Conference}} on {{High Performance Computing}} in {{Asia Pacific Region}}},
     author = {Pollinger, Theresa and Domke, Jens},
     date = {2026-01-25},
     year = {2026},
     series = {{{SCA}}/{{HPCAsia}} '26},
     publisher = {Association for Computing Machinery},
     location = {New York, NY, USA},
     doi = {10.1145/3773656.3773664},
     url = {https://dl.acm.org/doi/10.1145/3773656.3773664},
     data = {https://zenodo.org/records/15129650},
     urldate = {2026-02-19},
     isbn = {979-8-4007-2067-3}
   }

2025

1. CLUSTER ’25

   Towards High-Performance and Portable Molecular Docking on CPUs Through Vectorization

   Gianmarco Accordi, Jens Domke, Theresa Pollinger, and 2 more authors

   In 2025 IEEE International Conference on Cluster Computing (CLUSTER), 2025

   Abs DOI arXiv Bib Data

   Recent trends in the HPC field have introduced new CPU architectures with improved vectorization capabilities that require optimization to achieve peak performance and thus pose challenges for performance portability. The deployment of high-performing scientific applications for CPUs requires adapting the codebase and optimizing for performance. Evaluating these applications provides insights into the complex interactions between code, compilers, and hardware. We evaluate compiler auto-vectorization and explicit vectorization to achieve performance portability across modern CPUs with long vectors. We select a molecular docking application as a case study, as it represents computational patterns commonly found across HPC workloads. We report insights into the technical challenges, architectural trends, and optimization strategies relevant to the future development of scientific applications for HPC. Our results show which code transformations enable portable auto-vectorization, reaching performance similar to explicit vectorization. Experimental data confirms that x86 CPUs typically achieve higher execution performance than ARM CPUs, primarily due to their wider vectorization units. However, ARM architectures demonstrate competitive energy consumption and cost-effectiveness.

   @inproceedings{accordiHighPerformancePortableMolecular2025,
     title = {Towards {{High-Performance}} and {{Portable Molecular Docking}} on {{CPUs Through Vectorization}}},
     booktitle = {2025 {{IEEE International Conference}} on {{Cluster Computing}} ({{CLUSTER}})},
     author = {Accordi, Gianmarco and Domke, Jens and Pollinger, Theresa and Gadioli, Davide and Palermo, Gianluca},
     date = {2025-09},
     year = {2025},
     issn = {2168-9253},
     doi = {10.1109/CLUSTER59342.2025.11186493},
     url = {https://ieeexplore.ieee.org/abstract/document/11186493},
     urldate = {2025-10-13},
     data = {https://doi.org/10.5281/zenodo.14905033},
     eventtitle = {2025 {{IEEE International Conference}} on {{Cluster Computing}} ({{CLUSTER}})},
     keywords = {Benchmark testing,Codes,Energy consumption,Guidelines,Market research,Measurement,Optimization,Program processors,Proteins,Vectors}
   }

2. 

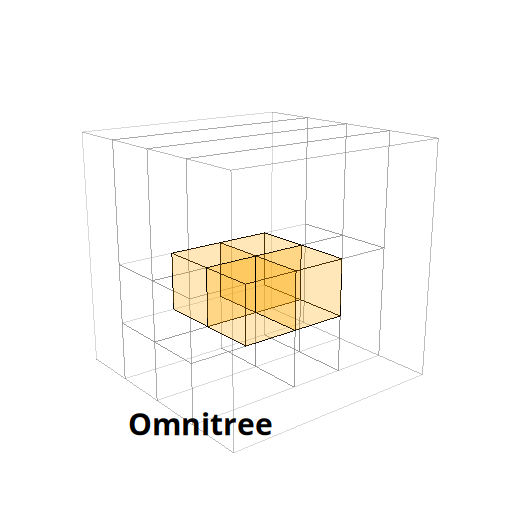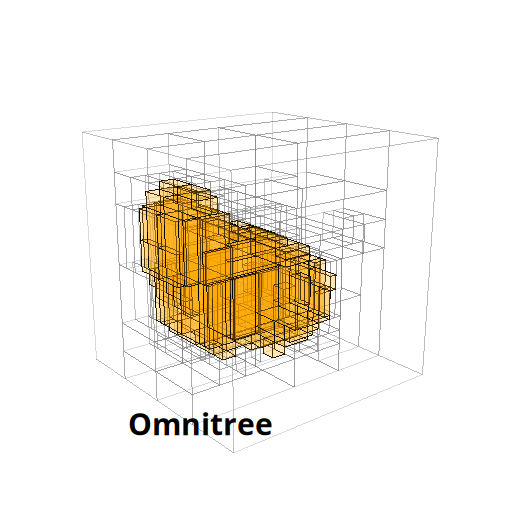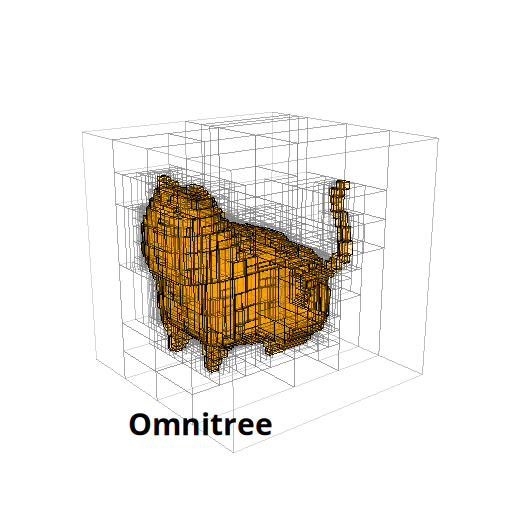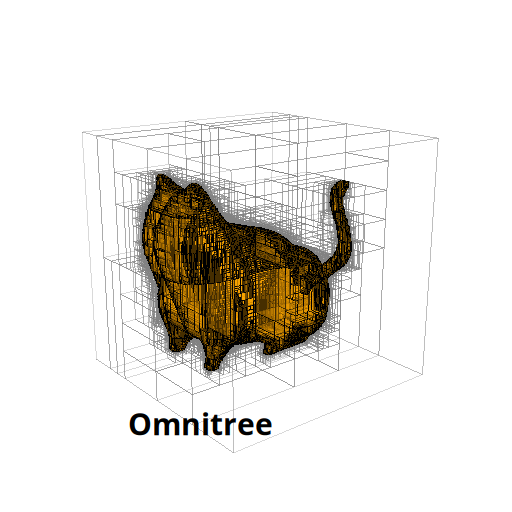   The Beauty of Anisotropic Mesh Refinement: Omnitrees for Efficient Dyadic Discretizations

   Theresa Pollinger, Masado Ishii, and Jens Domke

   2025

   Best Technical Poster at IMR26 Abs DOI arXiv Bib Code Poster Slides Data

   Our work about omnitrees was awarded the Best Technical Poster at IMR26!

   Structured adaptive mesh refinement (AMR), commonly implemented via quadtrees and octrees, underpins a wide range of applications including databases, computer graphics, physics simulations, and machine learning. However, octrees enforce isotropic refinement in regions of interest, which can be especially inefficient for problems that are intrinsically anisotropic–much resolution is spent where little information is gained. This paper presents omnitrees as an anisotropic generalization of octrees and related data structures. Omnitrees allow to refine only the locally most important dimensions, providing tree structures that are less deep than bintrees and less wide than octrees. As a result, the convergence of the AMR schemes can be increased by up to a factor of the dimensionality d for very anisotropic problems, quickly offsetting their modest increase in storage overhead. We validate this finding on the problem of binary shape representation across 4,166 three-dimensional objects: Omnitrees increase the mean convergence rate by 1.5x, require less storage to achieve equivalent error bounds, and maximize the information density of the stored function faster than octrees. These advantages are projected to be even stronger for higher-dimensional problems. We provide a first validation by introducing a time-dependent rotation to create four-dimensional representations, and discuss the properties of their 4-d octree and omnitree approximations. Overall, omnitree discretizations can make existing AMR approaches more efficient, and open up new possibilities for high-dimensional applications.

   @article{pollingerBeautyAnisotropicMesh2025,
     title = {The {{Beauty}} of {{Anisotropic Mesh Refinement}}: {{Omnitrees}} for {{Efficient Dyadic Discretizations}}},
     shorttitle = {Omnitrees for Efficient Dyadic Discretizations},
     author = {Pollinger, Theresa and Ishii, Masado and Domke, Jens},
     date = {2025-08-08},
     year = {2025},
     doi = {10.48550/arXiv.2508.06316},
     url = {http://arxiv.org/abs/2508.06316},
     urldate = {2025-08-12},
     pubstate = {accepted},
     langid = {english},
     keywords = {Computer Science - Computational Geometry,Computer Science - Data Structures and Algorithms,Computer Science - Graphics,Computer Science - Information Theory,Computer Science - Numerical Analysis,Mathematics - Information Theory,Mathematics - Numerical Analysis},
     data = {https://zenodo.org/records/15909872}
   }

3. JOSS

   DisCoTec: Distributed Higher-Dimensional HPC Simulations with the Sparse Grid Combination Technique

   Theresa Pollinger, Marcel Hurler, Alexander Van Craen, and 2 more authors

   Journal of Open Source Software, 2025

   Abs DOI Bib Code

   DisCoTec is a C++ framework for the sparse grid combination technique, designed for massively parallel settings. It is implemented with shared-memory parallelism via OpenMP and distributed-memory parallelism via MPI, and is intended to be used in conjunction with existing simulation codes. For simulation codes that can handle nested structured grids, little to no adaptation work is needed for use with the DisCoTec framework. The combination technique with DisCoTec demonstrates its superiority in precision-per-memory for higher-dimensional time-dependent simulations, such as high-fidelity plasma turbulence simulations in four to six dimensions and even for simulations in two dimensions, improvements can be observed. A central part of the combination technique at scale is the transformation of grid coefficients into a multi-scale basis. DisCoTec provides a selection of three different lifting wavelets for this purpose: hierachical hat basis, biorthogonal, and fullweighting basis. In addition, any code that can operate on nested structured grids can benefit from the model order reduction provided by the underlying sparse grid approach used by DisCoTec, without requiring any multi-scale operations. An additional feature of DisCoTec is the possibility of performing widely-distributed simulations of higher-dimensional problems, where multiple High-Performance Computing (HPC) systems collaborate to solve a joint simulation, as demonstrated in Pollinger et al. (2024). Thus, DisCoTec can leverage the compute power and main memory of multiple HPC systems, with comparatively low and manageable transfer costs due to the combination technique.

   @article{pollingerDisCoTecDistributedHigherdimensional2025,
     title = {{{DisCoTec}}: {{Distributed}} Higher-Dimensional {{HPC}} Simulations with the Sparse Grid Combination Technique},
     shorttitle = {{{DisCoTec}}},
     author = {Pollinger, Theresa and Hurler, Marcel and Craen, Alexander Van and Obersteiner, Michael and Pflüger, Dirk},
     date = {2025-02-26},
     year = {2025},
     journal = {Journal of Open Source Software},
     journaltitle = {Journal of Open Source Software},
     shortjournal = {JOSS},
     volume = {10},
     number = {106},
     pages = {7018},
     issn = {2475-9066},
     doi = {10.21105/joss.07018},
     url = {https://joss.theoj.org/papers/10.21105/joss.07018},
     urldate = {2025-04-02},
   }

2024

1. SC’24

   

   Realizing Joint Extreme-Scale Simulations on Multiple Supercomputers—Two Superfacility Case Studies

   Theresa Pollinger, Alexander Van Craen, Philipp Offenhäuser, and 1 more author

   In SC24: International Conference for High Performance Computing, Networking, Storage and Analysis, 2024

   Abs DOI Bib Data

   High-dimensional grid-based simulations serve as both a tool and a challenge in researching various domains. The main challenge of these approaches is the well-known curse of dimensionality, amplified by the need for fine resolutions in high-fidelity applications. The combination technique (CT) provides a straightforward way of performing such simulations while alleviating the curse of dimensionality. Recent work demonstrated the potential of the CT to join multiple systems simultaneously to perform a single high-dimensional simulation. This paper shows how to extend this to three or more systems and addresses some remaining challenges: load balancing on heterogeneous hardware; utilizing compression to maximize the communication bandwidth; efficient I/O management through hardware mapping; and improving memory utilization through algorithmic optimizations. Combining these contributions, we demonstrate the feasibility of the CT for extreme-scale Superfacility scenarios of 46 trillion DOF on two systems and 35 trillion DOF on three systems. Scenarios at these resolutions would be intractable with full-grid solvers (> 1,000 nonillion DOF each).

   @inproceedings{pollingerRealizingJointExtremeScale2024a,
     title = {Realizing {{Joint Extreme-Scale Simulations}} on {{Multiple Supercomputers}}—{{Two Superfacility Case Studies}}},
     booktitle = {{{SC24}}: {{International Conference}} for {{High Performance Computing}}, {{Networking}}, {{Storage}} and {{Analysis}}},
     author = {Pollinger, Theresa and Van Craen, Alexander and Offenhäuser, Philipp and Pflüger, Dirk},
     date = {2024-11},
     year = {2024},
     doi = {10.1109/SC41406.2024.00104},
     url = {https://ieeexplore.ieee.org/abstract/document/10793145},
     urldate = {2025-01-17},
     eventtitle = {{{SC24}}: {{International Conference}} for {{High Performance Computing}}, {{Networking}}, {{Storage}} and {{Analysis}}},
     keywords = {Analytical models,Bandwidth,combination technique,Computational modeling,coupling HPC systems,Couplings,file transfer,Hardware,High performance computing,higher-dimensional simulation,large scale,Load management,Load modeling,Memory management,multi-level methods,Optimization,plasma turbulence},
     data = {https://doi.org/10.18419/DARUS-3707}
   }

2. Stable and Mass-Conserving High-Dimensional Simulations with the Sparse Grid Combination Technique for Full HPC Systems and Beyond

   Theresa Pollinger

   2024

   Abs DOI Bib Data

   In the light of the ongoing climate crisis, mastering controlled plasma fusion has the potential to be one of the pivotal scientific achievements of the 21st century. To understand the turbulent fields in confined fusion devices, simulation has been and continues to be both an asset and a challenge. The main limiting factor to large-scale high-fidelity predictive simulations lies in the Curse of Dimensionality, which dominates all grid-based discretizations of plasmas based on the Vlasov-Poisson and Vlasov-Maxwell equations. In the full formulation, they result in six-dimensional grids and fine scales that need to be resolved, leading to a potentially untractable number of degrees of freedom. Typical approaches to this problem - coordinate transformations such as gyrokinetics, grid adaptation, restricting oneself to limited resolutions - do not directly address the Curse of Dimensionality, but rather work around it. The sparse grid combination technique, which forms the center of this work, is a multiscale approach that alleviates the curse of dimensionality for time-stepping simulations: Multiple regular grid-based simulations are run and update each other’s information throughout the course of simulation time. The present thesis improves upon the former state-of-the-art of the combination technique in three ways: introducing conservation of mass and numerical stability through the use of better-suited multiscale basis functions, optimizing the code for large-scale HPC systems, and extending the combination technique to the widely-distributed setting. Firstly, this thesis analyzes the often-used hierarchical hat function from the viewpoint of biorthogonal wavelets, which allows to replace the hierarchical hat function by other multiscale functions (such as the mass-conserving CDF wavelets) in a straightforward manner. Numerical studies presented in the thesis show that this not only introduces conservation but also increases accuracy and avoids numerical instabilities - which previously were a major roadblock for large-scale Vlasov simulations with the combination technique. Secondly, the open-source framework DisCoTec was extended to scale the combination technique up to the available memory of entire supercomputing systems. DisCoTec is designed to wrap the combination technique around existing grid-based solvers and draws on the inherent parallelism of the combination technique. Among several other contributions, different communication-avoiding multiscale reduction schemes were developed and implemented into DisCoTec as part of this work. The scalability of the approach is asserted by an extensive set of measurements in this thesis: DisCoTec is shown to scale up to the full system size of four German supercomputers, including the three CPU-based Tier-0/Tier-1 systems. Thirdly, the combination technique was further extended to the widely-distributed setting, where two HPC systems synchronously run a joint simulation. This is enabled by file transfer as well as sophisticated algorithms for assigning the different simulation instances to the systems, two of which were developed as part of this work. By the resulting drastic reductions in the communication volume, tolerable transfer times for combination technique simulations on different HPC systems have been achieved for the first time. These three advances - improved numerical properties, scaling efficiently up to full system sizes, and the possibility to extend the simulation beyond a single system - show the sparse grid combination technique to be a promising approach for future high-fidelity simulations of higher-dimensional problems, such as plasma turbulence.

   @thesis{pollingerStableMassconservingHighdimensional2024a,
     title = {Stable and Mass-Conserving High-Dimensional Simulations with the Sparse Grid Combination Technique for Full {{HPC}} Systems and Beyond},
     author = {Pollinger, Theresa},
     date = {2024},
     year = {2024},
     doi = {10.18419/opus-14210},
     url = {http://elib.uni-stuttgart.de/handle/11682/14229},
     urldate = {2024-04-14},
     isbn = {9781885727787},
     langid = {english},
     data = {https://doi.org/10.18419/DARUS-3580}
   }

2023

1. SC’23

   Leveraging the Compute Power of Two HPC Systems for Higher-Dimensional Grid-Based Simulations with the Widely-Distributed Sparse Grid Combination Technique

   Theresa Pollinger, Alexander Van Craen, Christoph Niethammer, and 2 more authors

   In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, New York, NY, USA, 2023

   Golden Spike Award Abs DOI Bib HTML Data

   Our work about joint simulations on multiple HPC systems was awarded the 2023 Golden Spike Award!

   Grid-based simulations of hot fusion plasmas are often severely limited by computational and memory resources; the grids live in four- to six-dimensional space and thus suffer the curse of dimensionality. However, high resolutions are required to fully capture the physics of interest. The sparse grid combination technique is a multi-scale method in which many anisotropically coarse resolved grids are used to approximate a fine-scale solution—and it alleviates the curse of dimensionality. This paper presents the core concepts of the widely-distributed combination technique, which allows us to use the compute power and memory of more than one HPC system for the same simulation. We apply the sparse grid combination technique to a six-dimensional advection problem serving as a proxy for plasma simulations. The full-grid solution approximated by the combination technique would contain ≈ 5 ZB if computed with conventional grid-based methods. Even the combination technique simulation operates on ≈ 1 × 1011 double-precision degrees of freedom, or 988 GB, plus the supporting sparse grid data structures. We propose a new approach to divide the compute load between the two HPC systems, requiring only 76 GB to be exchanged. Based on this, we have realized the first synchronous combination technique simulation using two HPC systems, in our case the two German Tier-0 supercomputers HAWK and SuperMUC-NG. On two systems, the simulation can be computed at an average overhead of ≈ 35 % (108 s per combination step) for file I/O and transfer. The presented concepts apply to any pair of HPC systems if high-speed data transfer is possible.

   @inproceedings{pollingerLeveragingComputePower2023b,
     title = {Leveraging the {{Compute Power}} of {{Two HPC Systems}} for {Higher-Dimensional} {Grid-Based} {Simulations} with the {{Widely-Distributed Sparse Grid Combination Technique}}},
     booktitle = {Proceedings of the {{International Conference}} for {{High Performance Computing}}, {{Networking}}, {{Storage}} and {{Analysis}}},
     author = {Pollinger, Theresa and Van Craen, Alexander and Niethammer, Christoph and Breyer, Marcel and Pflüger, Dirk},
     date = {2023-11-11},
     year = {2023},
     series = {{{SC}} '23},
     publisher = {Association for Computing Machinery},
     location = {New York, NY, USA},
     doi = {10.1145/3581784.3607036},
     url = {https://dl.acm.org/doi/10.1145/3581784.3607036},
     urldate = {2023-11-15},
     isbn = {979-8-4007-0109-2},
     keywords = {combination technique,coupling HPC systems,higher-dimensional simulation,multi-level methods,plasma turbulence,UFTP},
     data = {https://doi.org/10.18419/DARUS-3393}
   }

2. J. Comput. Phys.

   

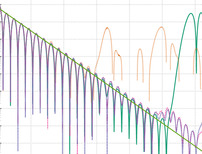   A Stable and Mass-Conserving Sparse Grid Combination Technique with Biorthogonal Hierarchical Basis Functions for Kinetic Simulations

   Theresa Pollinger, Johannes Rentrop, Dirk Pflüger, and 1 more author

   Journal of Computational Physics, 2023

   Abs DOI arXiv Bib Data

   The exact numerical simulation of plasma turbulence is one of the assets and challenges in fusion research. For grid-based solvers, sufficiently fine resolutions are often unattainable due to the curse of dimensionality. The sparse grid combination technique provides the means to alleviate the curse of dimensionality for kinetic simulations. However, the hierarchical representation for the combination step with the state-of-the-art hat functions suffers from poor conservation properties and numerical instability. The present work introduces two new variants of hierarchical multiscale basis functions for use with the combination technique: the biorthogonal and full weighting bases. The new basis functions conserve the total mass and are shown to significantly increase accuracy for a finite-volume solution of constant advection. Numerical analysis of the new basis functions reveals that their higher dual regularity does not only lead to conservation, but also yields an L2-stable basis for the combination technique. Accordingly, further numerical experiments applying the combination technique to a semi-Lagrangian Vlasov–Poisson solver in six dimensions show a stabilizing effect of the biorthogonal and full weighting bases on the simulations.

   @article{pollingerStableMassconservingSparse2023a,
     title = {A Stable and Mass-Conserving Sparse Grid Combination Technique with Biorthogonal Hierarchical Basis Functions for Kinetic Simulations},
     author = {Pollinger, Theresa and Rentrop, Johannes and Pflüger, Dirk and Kormann, Katharina},
     date = {2023-10-15},
     year = {2023},
     journal = {Journal of Computational Physics},
     journaltitle = {Journal of Computational Physics},
     shortjournal = {J. Comput. Phys.},
     volume = {491},
     issn = {0021-9991},
     doi = {10.1016/j.jcp.2023.112338},
     url = {https://www.sciencedirect.com/science/article/pii/S0021999123004333},
     urldate = {2023-07-26},
     langid = {english},
     keywords = {Kinetic simulations,Multi-scale functions,Numerical instabilities,Sparse grid combination technique,Vlasov–Poisson equations},
     data = {https://doi.org/10.18419/DARUS-2790}
   }

2022

1. Poster PASC’22

   Scaling the Plasma Simulation While Conserving the Mass: A Massively-Parallel Semi-Lagrangian Solver with the Sparse Grid Combination Technique

   Theresa Pollinger, Katharina Kormann, and Dirk Pflüger

   2022

   Best Poster Award Abs Bib Poster Data

   Our work about conservation in the combination technique was awarded the Best Poster Award at PASC’22!

   Grid-based direct plasma physics simulations suffer the curse of dimensionality in compute time and memory complexity, making the simulation of modern fusion devices extremely expensive and lengthy. Consequently, the curse also applies to the Semi-Lagrangian code selalib, which solves the 6-dimensional Vlasov-Poisson equation at high efficiency and scalability while conserving the plasma mass. The sparse grid combination technique can alleviate the curse of dimensionality, but former approaches have not respected the conservation of solver invariants such as mass. To overcome this limitation, the massively-parallel distributed combination technique code DisCoTec was extended to include two mass-preserving schemes, based on full weighting and biorthogonal wavelets. Our poster introduces the mass-conserving approach. It compares the DisCoTec+selalib solution with mass-conserving hierarchical functions to the standard hat function approach as well as the monolithic selalib solver on a full grid. Results are shown for a plasma two-stream instability in 6D. The full weighting and biorthogonal basis functions not only conserve the mass, but also stabilize the solution. This comes at a run time cost, since more data needs to be communicated. However, the extra parallelism introduced by the combination technique is not affected, allowing to still scale up to 8192 worker processes on Hawk.

   @unpublished{pollingerScalingPlasmaSimulation2022,
     type = {Poster},
     title = {Scaling the {{Plasma Simulation}} While {{Conserving}} the {{Mass}}: {{A Massively-Parallel Semi-Lagrangian Solver}} with the {{Sparse Grid Combination Technique}}},
     author = {Pollinger, Theresa and Kormann, Katharina and Pflüger, Dirk},
     date = {2022-06-25},
     year = {2022},
     url = {https://pasc22.pasc-conference.org/program/schedule/index.html%3Fpost_type=page&p=10&id=pos109&sess=sess181.html},
     urldate = {2022-07-19},
     langid = {american},
     venue = {PASC22},
     data = {https://doi.org/10.18419/DARUS-2784},
   }

2021

1. Beyond Fork-Join: Integration of Performance Portable Kokkos Kernels with HPX

   Gregor Daiß, Mikael Simberg, Auriane Reverdell, and 4 more authors

   In 2021 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), 2021

   Abs DOI Bib

   Between a widening range of GPU vendors and the trend of having more GPUs per compute node in supercomputers such as Summit, Perlmutter, Frontier and Aurora, developing performant yet portable distributed HPC applications becomes ever more challenging. Leveraging existing solutions like Kokkos for platform-independent code and HPX for distributing the application in a task-based fashion can alleviate these challenges. However, using such frameworks in the same application requires them to work together seamlessly. In this work we present an HPX Kokkos integration that works both ways: we can integrate CPU and GPU Kokkos kernels as HPX tasks and inversely use HPX worker threads to work on Kokkos kernels. Using HPX futures makes launching and synchronizing Kokkos kernels from multiple threads easy, allowing us to move away from the more traditional fork-join model. To evaluate our integrations we ported existing Vc and CUDA kernels within an existing HPX application, Octo-Tiger, to use Kokkos instead. We achieve comparable, or better, performance than with previous Vc and CUDA kernels, showing both the viability of our HPX Kokkos integration, as well as future-proofing Octo-Tiger for a wider range of potential machines. Furthermore, we introduce event polling for synchronizing CUDA kernels (or Kokkos kernels on the respective backend) achieving speedups over the previous solution using callbacks.

   @inproceedings{daissForkJoinIntegrationPerformance2021,
     title = {Beyond {{Fork-Join}}: {{Integration}} of {{Performance Portable Kokkos Kernels}} with {{HPX}}},
     shorttitle = {Beyond {{Fork-Join}}},
     booktitle = {2021 {{IEEE International Parallel}} and {{Distributed Processing Symposium Workshops}} ({{IPDPSW}})},
     author = {Daiß, Gregor and Simberg, Mikael and Reverdell, Auriane and Biddiscombe, John and Pollinger, Theresa and Kaiser, Hartmut and Pflüger, Dirk},
     date = {2021-06},
     year = {2021},
     pages = {377--386},
     doi = {10.1109/IPDPSW52791.2021.00066},
     eventtitle = {2021 {{IEEE International Parallel}} and {{Distributed Processing Symposium Workshops}} ({{IPDPSW}})},
     keywords = {CUDA,GPU,Graphics processing units,Hardware,HPX,Kernel,Kokkos,Performance Portability,Receivers,SIMD,Standardization,Supercomputers,Task-based Programming,Writing}
   }

2. Distributing Higher-Dimensional Simulations Across Compute Systems: A Widely Distributed Combination Technique

   Theresa Pollinger, Marcel Hurler, Michael Obersteiner, and 1 more author

   In 2021 IEEE/ACM International Workshop on Hierarchical Parallelism for Exascale Computing (HiPar), 2021

   Abs DOI Bib Data

   The numerical solution of high-dimensional PDE problems is essential for many research questions, such as understanding relativistic astrophysics, quantum physics, or hot fusion plasmas. At the same time, it is haunted by the curse of dimensionality, rendering finely resolved simulations infeasible even on modern architectures. The Sparse Grid Combination Technique helps to break the curse of dimensionality for high-dimensional PDE problems to some extent. But even then, simulations are restricted by the size of HPC systems. A new implementation based on the open-source code DisCoTec allows to distribute existing solvers even across compute systems: The widely distributed combination technique enables simulations at scales that would otherwise be intractable.This paper introduces the extended algorithm and showcases a proof of concept for the remote communication set-up. The scaling properties for the single-system and two-system cases are presented, and the numerical correctness of the implementation is validated.The widely distributed combination technique is useful in cases where the memory and/or compute resources are not sufficient for a particular problem to fit on one single available system, but multiple systems are able to accommodate it.

   @inproceedings{pollingerDistributingHigherDimensionalSimulations2021,
     title = {Distributing {{Higher-Dimensional Simulations Across Compute Systems}}: {{A Widely Distributed Combination Technique}}},
     shorttitle = {Distributing {{Higher-Dimensional Simulations Across Compute Systems}}},
     booktitle = {2021 {{IEEE}}/{{ACM International Workshop}} on {{Hierarchical Parallelism}} for {{Exascale Computing}} ({{HiPar}})},
     author = {Pollinger, Theresa and Hurler, Marcel and Obersteiner, Michael and Pflüger, Dirk},
     date = {2021-11},
     year = {2021},
     doi = {10.1109/HiPar54615.2021.00006},
     eventtitle = {2021 {{IEEE}}/{{ACM International Workshop}} on {{Hierarchical Parallelism}} for {{Exascale Computing}} ({{HiPar}})},
     keywords = {Codes,Computational modeling,Computer architecture,Conferences,Exascale computing,high dimensional simulation,Parallel processing,parallelism,Rendering (computer graphics),sparse grid combination technique},
     data = {https://doi.org/10.18419/DARUS-2123}
   }

2020

1. EXAHD: A Massively Parallel Fault Tolerant Sparse Grid Approach for High-Dimensional Turbulent Plasma Simulations

   Rafael Lago, Michael Obersteiner, Theresa Pollinger, and 6 more authors

   In , 2020

   Abs DOI Bib

   Plasma fusion is one of the promising candidates for an emission-free energy source and is heavily investigated with high-resolution numerical simulations. Unfortunately, these simulations suffer from the curse of dimensionality due to the five-plus-one-dimensional nature of the equations. Hence, we propose a sparse grid approach based on the sparse grid combination technique which splits the simulation grid into multiple smaller grids of varying resolution. This enables us to increase the maximum resolution as well as the parallel efficiency of the current solvers. At the same time we introduce fault tolerance within the algorithmic design and increase the resilience of the application code. We base our implementation on a manager-worker approach which computes multiple solver runs in parallel by distributing tasks to different process groups. Our results demonstrate good convergence for linear fusion runs and show high parallel efficiency up to 180k cores. In addition, our framework achieves accurate results with low overhead in faulty environments. Moreover, for nonlinear fusion runs, we show the effectiveness of the combination technique and discuss existing shortcomings that are still under investigation.

   @incollection{lagoEXAHDMassivelyParallel2020,
     title = {{{EXAHD}}: {{A Massively Parallel Fault Tolerant Sparse Grid Approach}} for {{High-Dimensional Turbulent Plasma Simulations}}},
     shorttitle = {{{EXAHD}}},
     author = {Lago, Rafael and Obersteiner, Michael and Pollinger, Theresa and Rentrop, Johannes and Bungartz, Hans-Joachim and Dannert, Tilman and Griebel, Michael and Jenko, Frank and Pflüger, Dirk},
     date = {2020-01-01},
     year = {2020},
     pages = {301--329},
     doi = {10.1007/978-3-030-47956-5_11},
     isbn = {978-3-030-47955-8}
   }

2. Learning-Based Load Balancing for Massively Parallel Simulations of Hot Fusion Plasmas

   Theresa Pollinger and Dirk Pflüger

   In Parallel Computing: Technology Trends, 2020

   Abs DOI Bib

   The sparse grid combination technique can be used to mitigate the curse of dimensionality and to gain insight into the physics of hot fusion plasmas with the gyrokinetic code GENE. With the sparse grid combination technique, massively parallel simulations can be performed on target resolutions that would be prohibitively large for standard full grid simulations. This can be achieved by numerically decoupling the target simulation into several smaller ones. Their time dependent evolution requires load balancing to obtain near optimal scaling beyond the scaling capabilities of GENE itself. This approach requires that good estimates for the runtimes exist. This paper revisits this topic for large-scale nonlinear global simulations and investigates common machine learning techniques, such as support vector regression and neural networks. It is shown that, provided enough data can be collected, load modeling by data-driven techniques can outperform expert knowledge-based fits — the current state-of-the-art approach.

   @incollection{pollingerLearningBasedLoadBalancing2020a,
     title = {Learning-{{Based Load Balancing}} for {{Massively Parallel Simulations}} of {{Hot Fusion Plasmas}}},
     author = {Pollinger, Theresa and Pflüger, Dirk},
     year = {2020},
     volume = {36},
     pages = {137--146},
     issn = {0927-5452},
     doi = {10.3233/APC200034},
     issue = {Parallel Computing: Technology Trends},
     booktitle = {Parallel {{Computing}}: {{Technology Trends}}},
     publisher = {IOS Press},
     url = {https://ebooks.iospress.nl/doi/10.3233/APC200034},
     langid = {english}
   }

2018

1. Knowledge Amalgamation for Computational Science and Engineering

   Theresa Pollinger, Michael Kohlhase, and Harald Köstler

   In Intelligent Computer Mathematics, Cham, 2018

   Abs DOI Bib Code

   This paper addresses a knowledge gap that is commonly encountered in computational science and engineering: To set up a simulation, we need to combine domain knowledge (usually in terms of physical principles), model knowledge (e.g. about suitable partial differential equations) with simulation (i.e. numerics/computing) knowledge. In current practice, this is resolved by intense collaboration between experts, which incurs non-trivial translation and communication overheads. We propose an alternate solution, based on mathematical knowledge management (MKM) techniques, specifically theory graphs and active documents: Given a theory graph representation of the domain, model, and background mathematics, we can derive a targeted knowledge acquisition dialogue that supports the formalization of domain knowledge, combines it with simulation knowledge and – in the end – drives a simulation run – a process we call MoSIS (“Models-to-Simulations Interface System”). We present the MoSIS prototype that implements this process based on a custom Jupyter kernel for the user interface and the theory-graph-based Mmt knowledge management system as an MKM backend.

   @inproceedings{pollingerKnowledgeAmalgamationComputational2018,
     title = {Knowledge {{Amalgamation}} for~{{Computational Science}} and~{{Engineering}}},
     booktitle = {Intelligent {{Computer Mathematics}}},
     author = {Pollinger, Theresa and Kohlhase, Michael and Köstler, Harald},
     editor = {Rabe, Florian and Farmer, William M. and Passmore, Grant O. and Youssef, Abdou},
     year = {2018},
     series = {Lecture {{Notes}} in {{Computer Science}}},
     pages = {232--247},
     publisher = {Springer International Publishing},
     location = {Cham},
     doi = {10.1007/978-3-319-96812-4_20},
     isbn = {978-3-319-96812-4},
     langid = {english},
   }